Dostředivé zrychlení

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
(+ Výrazné vylepšení)
m (Nahrazení textu „</math>“ textem „\)</big>“)
 
(Nejsou zobrazeny 3 mezilehlé verze.)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Dostředivé zrychlení|700}}
+
Při [[křivočarý pohyb|křivočarém pohybu]] je výhodné rozložit [[zrychlení]] do směru pohybu, tzn. do směru [[tečna|tečny]] k [[trajektorie|trajektorii]], a do směru [[Ortogonalita|kolmého]] k pohybu, tzn. do směru [[normála|normály]] k trajektorii. Hovoříme pak o '''[[tečné zrychlení|tečném zrychlení]]''' a '''normálovém''' (také '''dostředivém''') '''zrychlení'''.
 +
Směr [[Ortogonalita|kolmý]] k trajektorii je dán [[normála|normálou]] trajektorie a složka zrychlení, která má stejný směr jako tato normála, se označuje jako normálové zrychlení (hovoří se také o ''normálové složce zrychlení'') <big>\(\mathbf{a}_n\)</big>. Normálové zrychlení směřuje do středu [[první křivost|křivosti]] trajektorie, a proto se často nazývá dostředivým zrychlením a značí <big>\(\mathbf{a}_d\)</big>.
 +
 +
==Vektor a velikost normálového zrychlení==
 +
Pro velikost normálového zrychlení platí vztah
 +
:<big>\(a_n = \frac{\mathrm{d}v_n}{\mathrm{d}t} = \frac{v^2}{\rho}\)</big>,
 +
kde <big>\(\mathrm{d}v_n\)</big> je změna velikosti rychlosti ve směru [[normála|normály]] k [[trajektorie|trajektorii]] pohybu, <big>\(\mathbf{v}\)</big> je [[Rychlost|okamžitá rychlost]] a <big>\(\rho\)</big> je [[poloměr první křivosti|poloměr křivosti]] v daném [[bod]]ě [[trajektorie]].
 +
 +
Velikost dostředivého zrychlení závisí na rychlosti ([[Obvodová rychlost|obvodové]] nebo [[Úhlová rychlost|úhlové]]) a na poloměru zakřivení [[trajektorie]] (u [[Pohyb po kružnici|pohybu po kružnici]] na poloměru kružnice). Směr dostředivého zrychlení je do středu zakřivení (do středu kružnice) a je kolmý k vektoru rychlosti.
 +
 +
==Dostředivé zrychlení při rovnoměrném pohybu po kružnici==
 +
: ''Související informace naleznete také v článku'': [[Rovnoměrný pohyb po kružnici]]
 +
Při [[rovnoměrný pohyb po kružnici|rovnoměrném pohybu po kružnici]] je [[poloměr první křivosti|poloměr křivosti]] <big>\(\rho\)</big> roven [[poloměr]]u [[kružnice]] <big>\(r\)</big>. Použijeme-li navíc [[rychlost#Vztah mezi obvodovou a úhlovou rychlostí|vztah mezi obvodovou a úhlovou rychlostí]], pak pro velikost dostředivého zrychlení získáme vztah
 +
:<big>\(a_d = \frac{v^2}{r} = \omega^2 \cdot r \,\)</big>,
 +
kde ''v'' je velikost [[obvodová rychlost|obvodové rychlosti]], ''&omega;'' [[úhlová rychlost]], ''r'' je [[poloměr]] [[kružnice]].
 +
 +
===Odvození===
 +
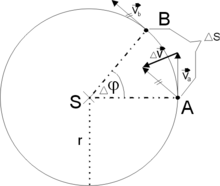
[[Soubor:Zrychlení.png|thumb|220px|K odvození velikosti dostředivého zrychlení]]
 +
:<big>\(\vec a = \frac {\Delta \vec v} {\Delta t}\)</big>
 +
:<big>\(\frac {v_a} {\Delta v} = \frac {r} {\Delta s}\)</big>
 +
Vzorec vyplývá z podobnosti rovnoramenných trojúhelníků se stejným vrcholovým úhlem, přičemž trajektorii <big>\( {\Delta s}\)</big>  aproximujeme přeponou AB, neboť ta se k trajektorii limitně blíží.
 +
:<big>\(v_a \cdot \Delta s = r \cdot \Delta v\)</big>
 +
:<big>\(\Delta v = \frac {v_a \cdot \Delta s} {r}\)</big>
 +
:<big>\(\frac {\Delta v} {\Delta t} = \frac {v_a} {r} \cdot \frac {\Delta s} {\Delta t}\)</big>
 +
Obě strany rovnice vydělíme <big>\( {\Delta t}\)</big>  a interpretujeme vzniklé derivace (diferenciály) jako zrychlení a rychlost.
 +
:<big>\(a = \frac {v_a} {r} \cdot v_a\)</big>
 +
:<big>\(\rightarrow a = \frac {v_a^2} {r} \Leftrightarrow a = \omega^2 \cdot r\)</big>
 +
 +
== Související články ==
 +
* [[Zrychlení]]
 +
* [[Tečné zrychlení]]
 +
* [[Dostředivá síla]]
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Kinematika]]
[[Kategorie:Kinematika]]
[[Kategorie:Zrychlení]]
[[Kategorie:Zrychlení]]

Aktuální verze z 14. 8. 2022, 14:51

Při křivočarém pohybu je výhodné rozložit zrychlení do směru pohybu, tzn. do směru tečny k trajektorii, a do směru kolmého k pohybu, tzn. do směru normály k trajektorii. Hovoříme pak o tečném zrychlení a normálovém (také dostředivém) zrychlení.

Směr kolmý k trajektorii je dán normálou trajektorie a složka zrychlení, která má stejný směr jako tato normála, se označuje jako normálové zrychlení (hovoří se také o normálové složce zrychlení) \(\mathbf{a}_n\). Normálové zrychlení směřuje do středu křivosti trajektorie, a proto se často nazývá dostředivým zrychlením a značí \(\mathbf{a}_d\).

Obsah

Vektor a velikost normálového zrychlení

Pro velikost normálového zrychlení platí vztah

\(a_n = \frac{\mathrm{d}v_n}{\mathrm{d}t} = \frac{v^2}{\rho}\),

kde \(\mathrm{d}v_n\) je změna velikosti rychlosti ve směru normály k trajektorii pohybu, \(\mathbf{v}\) je okamžitá rychlost a \(\rho\) je poloměr křivosti v daném bodě trajektorie.

Velikost dostředivého zrychlení závisí na rychlosti (obvodové nebo úhlové) a na poloměru zakřivení trajektorie (u pohybu po kružnici na poloměru kružnice). Směr dostředivého zrychlení je do středu zakřivení (do středu kružnice) a je kolmý k vektoru rychlosti.

Dostředivé zrychlení při rovnoměrném pohybu po kružnici

Související informace naleznete také v článku: Rovnoměrný pohyb po kružnici

Při rovnoměrném pohybu po kružnici je poloměr křivosti \(\rho\) roven poloměru kružnice \(r\). Použijeme-li navíc vztah mezi obvodovou a úhlovou rychlostí, pak pro velikost dostředivého zrychlení získáme vztah

\(a_d = \frac{v^2}{r} = \omega^2 \cdot r \,\),

kde v je velikost obvodové rychlosti, ω úhlová rychlost, r je poloměr kružnice.

Odvození

K odvození velikosti dostředivého zrychlení
\(\vec a = \frac {\Delta \vec v} {\Delta t}\)
\(\frac {v_a} {\Delta v} = \frac {r} {\Delta s}\)

Vzorec vyplývá z podobnosti rovnoramenných trojúhelníků se stejným vrcholovým úhlem, přičemž trajektorii \( {\Delta s}\) aproximujeme přeponou AB, neboť ta se k trajektorii limitně blíží.

\(v_a \cdot \Delta s = r \cdot \Delta v\)
\(\Delta v = \frac {v_a \cdot \Delta s} {r}\)
\(\frac {\Delta v} {\Delta t} = \frac {v_a} {r} \cdot \frac {\Delta s} {\Delta t}\)

Obě strany rovnice vydělíme \( {\Delta t}\) a interpretujeme vzniklé derivace (diferenciály) jako zrychlení a rychlost.

\(a = \frac {v_a} {r} \cdot v_a\)
\(\rightarrow a = \frac {v_a^2} {r} \Leftrightarrow a = \omega^2 \cdot r\)

Související články


Citováno z „http://www.multimediaexpo.cz/mmecz/index.php/Dost%C5%99ediv%C3%A9_zrychlen%C3%AD“