Vlnová rovnice

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Verze z 13. 6. 2021, 08:33

Vlnová rovnice je významnou hyperbolickou parciální diferenciální rovnicí druhého řádu, která popisuje celou řadu vlnění, ať už v akustice, optice, elektromagnetismu, nebo v mechanice při popisu strun nebo kapalin. Jako vlnovou rovnici označujeme rovnici, kterou lze vyjádřit ve tvaru

Puls na struně s upevněnými konci modelovaný jednorozměrnou vlnovou rovnicí.

<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \frac{\partial^2 z}{\partial x_1^2} + \frac{\partial^2 z}{\partial x_2^2} + ... + \frac{\partial^2 z}{\partial x_n^2},</math>

což bývá zpravidla ekvivalentně zapisováno pomocí laplaceova operátoru jako

<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \Delta z.</math>

<math>z</math> přitom představuje skalární funkci polohy a času.

Pod pojmem vlnová rovnice je obvykle myšlena homogenní rovnice. V obecnějším tvaru má vlnová rovnice nehomogenní vyjádření

<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \Delta z + f(x_1,x_2,...,x_n)</math>

Při popisu vlnění se pojem vlnová rovnice užívá k označení diferenciální rovnice, která charakterizuje dynamiku daného vlnění. V takovém případě může být označení vlnová rovnice použito pro libovolnou (i nelineární) diferenciální rovnici.

Související články

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 1: / Řádka 1: @@
-{{Wikipedia-cs|Vlnová rovnice|700}}
+'''Vlnová rovnice''' je významnou [[hyperbolická diferenciální rovnice|hyperbolickou]] [[parciální diferenciální rovnice|parciální diferenciální rovnicí]] druhého řádu, která popisuje celou řadu [[vlnění]], ať už v [[akustika|akustice]], [[optika|optice]], [[elektromagnetismus|elektromagnetismu]], nebo v [[mechanika|mechanice]] při popisu [[struna|strun]] nebo [[kapalina|kapalin]]. Jako vlnovou rovnici označujeme [[parciální diferenciální rovnice|rovnici]], kterou lze vyjádřit ve tvaru
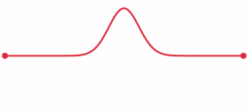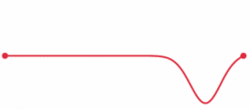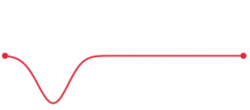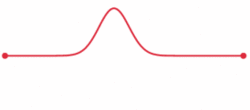
+[[Soubor:Wave equation 1D fixed endpoints.gif|thumb|250px|Puls na struně s upevněnými konci modelovaný jednorozměrnou vlnovou rovnicí.]]
+:<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \frac{\partial^2 z}{\partial x_1^2} + \frac{\partial^2 z}{\partial x_2^2} + ... + \frac{\partial^2 z}{\partial x_n^2},</math>
+což bývá zpravidla ekvivalentně zapisováno pomocí [[Laplaceův operátor|laplaceova operátoru]] jako
+:<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \Delta z.</math>
+<math>z</math> přitom představuje skalární funkci [[poloha|polohy]] a [[čas]]u.
+Pod pojmem vlnová rovnice je obvykle myšlena homogenní rovnice. V obecnějším tvaru má vlnová rovnice nehomogenní vyjádření
+:<math>\frac{1}{c^2}\frac{\partial^2 z}{\partial t^2} = \Delta z + f(x_1,x_2,...,x_n)</math>
+Při popisu [[vlnění]] se pojem ''vlnová rovnice'' užívá k označení [[diferenciální rovnice]], která charakterizuje dynamiku daného vlnění. V takovém případě může být označení vlnová rovnice použito pro libovolnou (i [[nelineární diferenciální rovnice|nelineární]]) diferenciální rovnici.
+== Související články ==
+* [[Hyperbolická diferenciální rovnice]]
+* [[Laplaceův operátor]]
+* [[Vlnění]]
+* [[Sférická vlna]]
+* [[Rovinná vlna]]
+{{Článek z Wikipedie}}
+[[Kategorie:Diferenciální počet]]
+[[Kategorie:Rovnice]]
+[[Kategorie:Vlnění]]
 [[Kategorie:Diferenciální počet]]
 [[Kategorie:Rovnice]]
 [[Kategorie:Vlnění]]