Teorie grafů
Z Multimediaexpo.cz
m (Nahrazení textu) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Nejsou zobrazeny 2 mezilehlé verze.) | |||
| Řádka 1: | Řádka 1: | ||
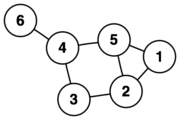
[[Soubor:6n-graf.png|thumb|Graf se šesti vrcholy.]] | [[Soubor:6n-graf.png|thumb|Graf se šesti vrcholy.]] | ||
'''Teorie grafů''' zkoumá vlastnosti struktur, zvaných [[Graf (teorie grafů)|grafy]]. Ty jsou tvořeny vrcholy, které jsou vzájemně spojené hranami. Znázorňuje se obvykle jako množina bodů spojených čárami. Formálně je graf uspořádanou dvojicí množiny vrcholů V a množiny hran E: | '''Teorie grafů''' zkoumá vlastnosti struktur, zvaných [[Graf (teorie grafů)|grafy]]. Ty jsou tvořeny vrcholy, které jsou vzájemně spojené hranami. Znázorňuje se obvykle jako množina bodů spojených čárami. Formálně je graf uspořádanou dvojicí množiny vrcholů V a množiny hran E: | ||
| - | :< | + | :<big>\(G = \left( V, E \right)\)</big> |
Pomocí grafů lze reprezentovat struktury a úlohy z nejrůznějších oborů. Taktéž mnoho problémů praktického života může být formulováno jako úloha teorie grafů - kupříkladu struktura vzájemného propojení článků Wikipedie. Jednotlivé články jsou vrcholy grafu a odkaz z článku A na článek B je [[orientovaný graf|orientovanou hranou]] mezi vrcholy A a B. | Pomocí grafů lze reprezentovat struktury a úlohy z nejrůznějších oborů. Taktéž mnoho problémů praktického života může být formulováno jako úloha teorie grafů - kupříkladu struktura vzájemného propojení článků Wikipedie. Jednotlivé články jsou vrcholy grafu a odkaz z článku A na článek B je [[orientovaný graf|orientovanou hranou]] mezi vrcholy A a B. | ||
Struktura grafu může být rozšířena o ohodnocení hran (také označováno jako váha; může reprezentovat délku, náklady na přesun, průchodnost apod.) nebo vrcholu. Výsledkem je model reálné sítě. Takové modely se používají pro analýzu dopravy nebo počítačových sítí (jako např. internetu). | Struktura grafu může být rozšířena o ohodnocení hran (také označováno jako váha; může reprezentovat délku, náklady na přesun, průchodnost apod.) nebo vrcholu. Výsledkem je model reálné sítě. Takové modely se používají pro analýzu dopravy nebo počítačových sítí (jako např. internetu). | ||
Aktuální verze z 14. 8. 2022, 14:53
Teorie grafů zkoumá vlastnosti struktur, zvaných grafy. Ty jsou tvořeny vrcholy, které jsou vzájemně spojené hranami. Znázorňuje se obvykle jako množina bodů spojených čárami. Formálně je graf uspořádanou dvojicí množiny vrcholů V a množiny hran E:
- \(G = \left( V, E \right)\)
Pomocí grafů lze reprezentovat struktury a úlohy z nejrůznějších oborů. Taktéž mnoho problémů praktického života může být formulováno jako úloha teorie grafů - kupříkladu struktura vzájemného propojení článků Wikipedie. Jednotlivé články jsou vrcholy grafu a odkaz z článku A na článek B je orientovanou hranou mezi vrcholy A a B. Struktura grafu může být rozšířena o ohodnocení hran (také označováno jako váha; může reprezentovat délku, náklady na přesun, průchodnost apod.) nebo vrcholu. Výsledkem je model reálné sítě. Takové modely se používají pro analýzu dopravy nebo počítačových sítí (jako např. internetu).
Historie
Tradičně se za zakladatele teorie grafů považuje Leonhard Euler, který roku 1736 řešil úlohu, jak projít přes sedm mostů v Královci (každý z nich právě jednou) a vrátit se do výchozího místa. To v moderní teorii odpovídá pojmu eulerovský graf. V roce 1845 publikoval Gustav Kirchhoff zákony, které platí v elektrických obvodech a slouží k výpočtu napětí a proudu v jednotlivých větvích obvodu. V teorii grafů našly své uplatnění při studiu tzv. toků v sítích. V roce 1852 předložil Francis Guthrie takzvaný problém čtyř barev - tedy otázku, zda je možné obarvit libovolnou mapu pomocí nejvýše čtyř barev tak, aby každé dvě sousední země (které mají společnou hranici delší než jediný bod) měly odlišnou barvu. Byl vyřešen až o více než sto let později, přičemž pro jeho řešení bylo zavedeno mnoho zásadních konceptů teorie grafů (viz rovinný graf).
Úlohy
Velké množství úloh z teorie grafů je NP-úplných, mezi nimi např.:
- hledání největšího úplného podgrafu – tzv. problém kliky,
- hledání největší nezávislé množiny,
- problém obchodního cestujícího
Z dalších je to například
- problém čtyř barev,
- hledání minimální kostry grafu.
Externí odkazy
- Java applety demonstrující některé algoritmy z teorie grafů
- Teorie grafů - Bc. práce z MFF UK zabývající se historií teorie grafů a úvodem, obsahuje základní definice, vybrané problémy a algoritmy včetně animací a kódů v Pascalu
- [1] - J.A.Bondy,
U.S.R. Murty: Graph Theory with Applications, Springer 2008. - monografie
- [2] - R.Diestel: Graph Theory, Springer 2005. - monografie, stredne pokrocili.
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |