The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Norma (matematika)
Z Multimediaexpo.cz
Norma je funkce, která každému nenulovému vektoru přiřazuje kladné reálné číslo (tzv. délku nebo velikost), nulový vektor jako jediný má délku 0.
V případě seminormy se naopak připouští, aby i nenulovým vektorům byla přiřazena nulová délka.
Obsah |
Definice
Nechť V je vektorový prostor nad nějakým podtělesem F tělesa komplexních čísel a p je reálná funkce definovaná na V. Funkce p je seminorma na V, jestliže je
- pozitivně homogenní: p(a v) = |a| p(v), pro a ∈ F a v ∈ V;
- subaditivní: p(u + v) ≤ p(u) + p(v), pro u, v ∈ V.
Z předpokladu pozitivní homogenity plyne, že p(0) = 0 a následně ze subaditivity p(v) ≥ 0, pro všechna v ∈ V.
Norma je seminorma p, která je navíc pozitivně definitní:
- p(v) = 0 právě tehdy, když v = 0.
Pro normu se namísto p(v) zpravidla používá označení ||v||.
Příklady
- Každá norma je seminorma.
- Absolutní hodnota je norma na reálných číslech.
- Každá lineární forma f na vektorovém prostoru definuje seminormu x → |f(x)|.
Eukleidovská norma
Na prostoru \(\mathbb{R}^n\) lze definovat tzv. eukleidovskou normu vektoru x = (x1, x2, ..., xn) jako
- \(\|\mathbf{x}\| := \sqrt{x_1^2 + \cdots + x_n^2}.\)
Tato norma udává vzdálenost bodu x od počátku (což je důsledek Pythagorovy věty).
p-norma
Nechť p ≥ 1 je reálné číslo.
- \(\|\textbf{x}\|_p := \left( \sum_{i=1}^n |x_i|^p \right)^\frac{1}{p}.\)
Eukleidovská norma je speciálním případem této normy (pro p = 2).
Maximová norma
- \(\|\textbf{x}\|_\infty := \max \left(|x_1|, \ldots ,|x_n| \right).\)
Norma na prostoru se skalárním součinem
Skalární součin indukuje přirozeným způsobem normu
- \(\|x\| := \sqrt{(x,x)}.\)
Pro normu indukovanou skalárním součinem platí Cauchyho–Schwarzova nerovnost
- \( |(x,y)| \leq \|x\| \, \|y\|.\)
Vlastnosti
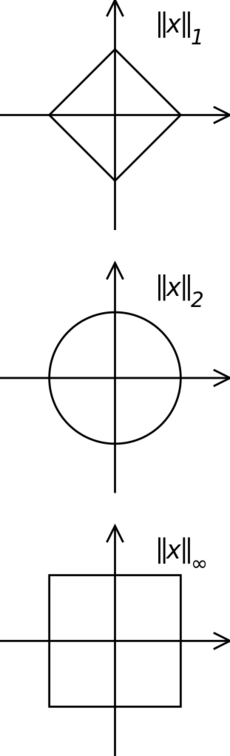
Tvar jednotkové kružnice (množiny vektorů velikosti 1) se liší v různých normách (viz ilustraci).
Normy ||•||α and ||•||β na vektorovém prostoru V se nazývají ekvivalentní, jestliže existují kladná reálná čísla C a D taková, že
- \(C\|x\|_\alpha\leq\|x\|_\beta\leq D\|x\|_\alpha\)
pro všechna x ∈ V. Na vektorovém prostoru konečné dimenze jsou všechny normy ekvivalentní. Například normy ||•||1, ||•||2 a ||•||∞ jsou ekvivalentní na prostoru \(\mathbb{R}^n\):
- \(\|x\|_2\le\|x\|_1\le\sqrt{n}\|x\|_2,\)
- \(\|x\|_\infty\le\|x\|_2\le\sqrt{n}\|x\|_\infty,\)
- \(\|x\|_\infty\le\|x\|_1\le n\|x\|_\infty.\)
Ekvivalentní normy indukují tutéž topologii. Jsou-li dány dvě ekvivalentní normy na jednom prostoru, pak je spojitost funkcí i konvergence posloupností z tohoto prostoru v obou normách stejná.
Konvexní, vyvážené, pohlcující množiny
Seminormy jsou úzce spjaty s konvexními, vyváženými, pohlcujícími množinami.
Nechť p je seminorma na vektorovém prostoru V, pak pro libovolný skalár α jsou množiny {x : p(x) < α} a {x : p(x) ≤ α} konvexní, vyvážené a pohlcující.
Obráceně, ke každé konvexní, vyvážené, pohlcující podmnožině C prostoru V existuje seminorma μC známá jako Minkowského funkcionál množiny C, definovaná
- \(\mu_C(x) := \inf\{\alpha : \alpha > 0, x \in \alpha C\}.\)
Pro tuto seminormu platí
- \(\{x : \mu_C(x) < 1\} \subseteq C \subseteq \{x : \mu_C(x) \leq 1\}.\)
Související články
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |