The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Kvadratická funkce
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 1: | Řádka 1: | ||
| - | [[File:Polynomialdeg2.png|thumb|230px|<center><big>\(x^2 - x - 2\!</ | + | [[File:Polynomialdeg2.png|thumb|230px|<center><big>\(x^2 - x - 2\!\)</big></center>]] |
'''Kvadratická funkce''' je taková [[Funkce (matematika)|funkce]], jejíž hodnota se mění úměrně druhé [[Umocňování|mocnině]] nezávislé [[proměnná|proměnné]]. | '''Kvadratická funkce''' je taková [[Funkce (matematika)|funkce]], jejíž hodnota se mění úměrně druhé [[Umocňování|mocnině]] nezávislé [[proměnná|proměnné]]. | ||
| - | Například funkce <big>\(y = -2x^2 + 5x + {1 \over 2}</ | + | Například funkce <big>\(y = -2x^2 + 5x + {1 \over 2}\)</big> je kvadratická. |
| - | Ryze kvadratická funkce je pak funkce bez lineárního členu x, například <big>\(y = 3x^2 - 10</ | + | Ryze kvadratická funkce je pak funkce bez lineárního členu x, například <big>\(y = 3x^2 - 10\)</big>. |
== Definice == | == Definice == | ||
| - | Funkce ''f'' je kvadratická, pokud ji lze vyjádřit ve tvaru <big>\(f(x) = a \cdot x^2 + b \cdot x + c</ | + | Funkce ''f'' je kvadratická, pokud ji lze vyjádřit ve tvaru <big>\(f(x) = a \cdot x^2 + b \cdot x + c\)</big>,<br />kde ''a'', ''b'' i ''c'' jsou [[konstanta|konstanty]] a <big>\(a \ne 0\)</big>. |
| - | [[Definiční obor]] kvadratické funkce je <big>\(( - \infty, \infty )</ | + | [[Definiční obor]] kvadratické funkce je <big>\(( - \infty, \infty )\)</big>. |
== Vlastnosti == | == Vlastnosti == | ||
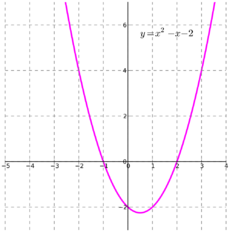
* [[graf (funkce)|grafem]] kvadratické funkce je [[Parabola (matematika)|parabola]] | * [[graf (funkce)|grafem]] kvadratické funkce je [[Parabola (matematika)|parabola]] | ||
* kvadratická funkce má v každém bodě [[derivace|derivaci]] | * kvadratická funkce má v každém bodě [[derivace|derivaci]] | ||
| - | ** příklad: funkce <big>\(f(x) = 5x^2 + 3x - 6</ | + | ** příklad: funkce <big>\(f(x) = 5x^2 + 3x - 6\)</big> má derivaci <big>\(f'(x) = 10x + 3\)</big> |
* [[primitivní funkce]] ke kvadratické funkci je funkce [[kubická funkce|kubická]] | * [[primitivní funkce]] ke kvadratické funkci je funkce [[kubická funkce|kubická]] | ||
| - | ** příklad: <big>\(\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C</ | + | ** příklad: <big>\(\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C\)</big> |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:52
Kvadratická funkce je taková funkce, jejíž hodnota se mění úměrně druhé mocnině nezávislé proměnné.
Například funkce \(y = -2x^2 + 5x + {1 \over 2}\) je kvadratická.
Ryze kvadratická funkce je pak funkce bez lineárního členu x, například \(y = 3x^2 - 10\).
Definice
Funkce f je kvadratická, pokud ji lze vyjádřit ve tvaru \(f(x) = a \cdot x^2 + b \cdot x + c\),
kde a, b i c jsou konstanty a \(a \ne 0\).
Definiční obor kvadratické funkce je \(( - \infty, \infty )\).
Vlastnosti
- grafem kvadratické funkce je parabola
- kvadratická funkce má v každém bodě derivaci
- příklad: funkce \(f(x) = 5x^2 + 3x - 6\) má derivaci \(f'(x) = 10x + 3\)
- primitivní funkce ke kvadratické funkci je funkce kubická
- příklad: \(\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |