The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Lineární rovnice
Z Multimediaexpo.cz
Termín lineární rovnice v matematice označuje algebraickou rovnici prvního stupně, tzn. rovnici o jedné neznámé, ve které neznámá vystupuje pouze v první mocnině. V základním tvaru vypadá následovně:
- \(ax + b = 0\)
Zde jsou a a b nějaká reálná čísla, tzv. koeficienty této rovnice (a se nazývá lineární koeficient, b je absolutní člen), x je neznámá. a je různé od nuly, neboť pro a=0 se jedná o triviální rovnici b = 0, která buď nemá řešení (pokud je číslo b nenulové), nebo jsou jejím řešením všechna reálná čísla (pokud je b nula).
Řešení rovnice
Lineární rovnice se řeší prostým osamostatněním neznámé x: převedením b na opačnou stranu a vydělením rovnice číslem a. Řešením je tedy
- \(x = \frac{-b}{a}\).
Geometrický význam
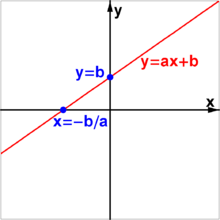
Levá strana rovnice (ax + b) popisuje přímku. Při řešení rovnice hledáme průsečík této přímky s osou x. Přímka v rovině může mít vůči ose x obecně tři polohy:
- Přímka je totožná s osou x. Její rovnice je tudíž y = 0, koeficienty příslušné lineární rovnice jsou a = 0, b = 0. Řešením rovnice jsou všechna reálná čísla.
- Přímka je rovnoběžná s osou x, ale je od ní různá. Její rovnice je y = k, přičemž k je nenulové. Koeficienty příslušné lineární rovnice jsou a = 0, b = k ≠ 0. Jelikož různé rovnoběžné přímky nemají průsečík, rovnice nemá řešení.
- Přímka je s osou x různoběžná. Její rovnice je y = ax + b, přičemž a je nenulové (výjimečným případem je situace, kdy přímka je kolmá na osu x a její rovnice má tvar x = k). Tehdy má přímka s osou x jeden průsečík a rovnice má jedno řešení.
Související články
- Kvadratická rovnice
- Kubická rovnice
- Kvartická rovnice
- Binomická rovnice
- Lineární diferenciální rovnice
- Lineární integrální rovnice
- Soustava lineárních rovnic
- Soustava rovnic
- Rovnice
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |