Přímka

Z Multimediaexpo.cz

Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl.

Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“). V euklidovské geometrii pro každé dva body existuje právě jedna přímka, která oběma prochází. Tato přímka představuje nejkratší spojnici mezi dotyčnými body. Z fyzikálního hlediska je přímka trajektorie fotonu neovlivněného gravitací. Speciální případ přímky je osa.

Obsah 1 Značení 2 Algebraický zápis 2.1 Rovinná přímka 2.1.1 Směrnicová rovnice přímky 2.1.2 Úseková rovnice přímky 2.1.3 Normálová rovnice přímky 2.1.4 Obecná rovnice přímky 2.1.5 Parametrické rovnice přímky 2.1.6 Vektorová rovnice přímky 2.1.7 Polární rovnice přímky 2.1.8 Rovnice přímky určené bodem 2.2 Prostorová přímka 2.2.1 Obecná rovnice přímky 2.2.2 Parametrické rovnice přímky 2.2.3 Rovnice přímky určené bodem 2.3 Přímka ve vícerozměrném prostoru 2.3.1 Parametrické vyjádření 2.3.2 Vektorový tvar 3 Vzájemná poloha bodu a přímky 4 Vzájemná poloha přímek 5 Související články

Značení

Přímka se znázorňuje rovnou čarou, označuje se malým písmenem, např. \(a, b, c, ...\). Přímka procházející dvěma body \(A,B\) bývá také značena \(\begin{matrix} \leftrightarrow \\ AB \\ \end{matrix}\). Znázornění: Soubor:Přímka.png

Algebraický zápis

Přímku v rovině lze algebraicky popsat pomocí lineárních rovnic nebo lineárních funkcí. Tento intuitivní koncept přímky lze formalizovat několika způsoby. Jestliže je geometrie postavena axiomaticky (jako v Eukleidových Základech a později ve Foundations of Geometry Davida Hilberta), potom přímky nejsou vůbec definovány, nýbrž axiomaticky charakterizovány svými vlastnostmi. „Vše, co splňuje axiomy pro přímku, je přímka.“ Zatímco Eukleidés definoval přímku jako „délku bez šířky“, ve svých pozdějších vývodech tuto mlhavou definici nepoužíval. V Eukleidovském prostoru Rⁿ (a analogicky ve všech ostatních vektorových prostorech) definujeme přímku L jako podmnožinu ve tvaru

\(L = \{\mathbf{a}+t\mathbf{b}\mid t\in\mathbb{R}\}\)

kde a a b jsou vektory v Rⁿ a b je nenulové. Vektor b udává směr přímky a a je bod na přímce. Tutéž přímku lze definovat pomocí různých kombinací a a b.

Rovinná přímka

V R² je každá přímka L popsaná lineární rovnicí, která může být zadána v různých tvarech.

Směrnicová rovnice přímky

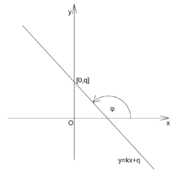
Směrnicová rovnice přímky má tvar

\(y=kx+q\),

kde \(k = \operatorname{tg}\varphi\) je tzv. směrnice přímky, přičemž \(\varphi\) je orientovaný úhel s vrcholem v průsečíku přímky a první souřadnicové osy, jehož rameny jsou (kladně orientovaná) první osa souřadnicové soustavy a přímka, a \(q\) je tzv. úsek (vyťatý přímkou) na ose \(y\), což je druhá souřadnice průsečíku přímky s osou \(y\). Pro \(k>0\) představuje rovnice přímky rostoucí funkci, pro \(k<0\) jde o funkci klesající. Pro \(k=0\) je přímka rovnoběžná s osou \(x\). Je-li \(q=0\), pak přímka prochází počátkem \(O\). Přímku rovnoběžnou s osou \(y\) nelze směrnicovou rovnicí vyjádřit.

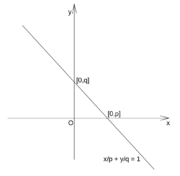
Úseková rovnice přímky

Úseková rovnice přímky má tvar

\(\frac{x}{p}+\frac{y}{q} = 1\),

kde \(p\neq 0\) je úsek (vyťatý přímkou) na ose \(x\) a \(q\neq 0\) je úsek (vyťatý přímkou) na ose \(y\). Přímku rovnoběžnou s osou \(x\) nebo \(y\) nelze úsekovou rovnicí vyjádřit.

Normálová rovnice přímky

Normálovou rovnici přímky lze zapsat va tvaru

\(x \cos\psi + y \sin\psi - n = 0\),

kde \(n\geq 0\) představuje vzdálenost počátku soustavy souřadnic \(O\) od přímky a \(\psi\) je velikost orientovaného úhlu, jehož rameno je první kladná poloosa souřadné soustavy a druhé rameno je polopřímka s počátkem v \(O\) vedená kolmo k přímce. Členy \(\cos\psi\) a \(\sin\psi\) představují složky jednotkového vektoru kolmého k přímce.

Obecná rovnice přímky

Obecná rovnice přímky má tvar

\(ax+by+c=0\),

kde \(a, b, c\) jsou konstanty, přičemž \(a\neq 0\) nebo \(b\neq 0\). Pro \(a=0\) je přímka rovnoběžná s osou \(x\), pro \(b=0\) je přímka rovnoběžná s osou \(y\). Pro \(c=0\) prochází přímka počátkem. Porovnáním obecné a normálové rovnice lze určit význam konstant \(a, b, c\). Konstanty \(a, b\) určují vektor \(\mathbf{n}\), který je kolmý k přímce. Parametr \(c\) pak souvisí se vzdáleností přímky od počátku souřadné soustavy. Obecnou rovnici přímky lze převést na rovnici směrnicovou, pokud zavedeme \(k=-\frac{a}{b}, q=-\frac{c}{b}\), pro \(b\neq 0\). Zavedeme-li \(p=-\frac{c}{a}, q=-\frac{c}{b}\), pro \(a\neq 0, b\neq 0, c\neq 0\), pak můžeme obecnou rovnici převést na úsekový tvar. Převedením obecné rovnice přímky do normálového tvaru získáme normálovou rovnici přímky ve tvaru

\(\frac{a}{\sqrt{a^2+b^2}{\operatorname{sgn}}{c}}x + \frac{b}{\sqrt{a^2+b^2}{\operatorname{sgn}}{c}}y + \frac{c}{\sqrt{a^2+b^2}{\operatorname{sgn}}{c}} = 0\)

Důležité vlastnosti takto definovaných přímek jsou jejich sklon, x-intercept a y-intercept. Excentricita přímky je nekonečno.

Parametrické rovnice přímky

Parametrické rovnice přímky v rovině lze vyjádřit vztahy

\(x = x_0 + a_1 t\)

\(y = y_0 + a_2 t\)

kde \([x_0,y_0]\) je libovolný bod přímky, \(a_1, a_2\) jsou konstanty určující směrnici přímky a \(t\in (-\infty,\infty)\) je proměnný parametr. Alespoň jedna z konstant \(a_1, a_2\) musí být nenulová.

Vektorová rovnice přímky

Vektorová rovnice přímky má tvar

\(\mathbf{r} = \mathbf{r}_0 + \mathbf{a} t\)

kde \(\mathbf{r}\) je rádiusvektor procházející všemi body přímky, \(\mathbf{r}_0\) je rádiusvektor jednoho z bodů přímky, \(\mathbf{a}\) je vektor určující směr přímky a \(t\in(-\infty,\infty)\) je proměnný parametr. Vektorový zápis tedy představuje přehlednější zápis parametrického tvaru rovnice přímky.

Polární rovnice přímky

V polárních souřadnicích lze přímku vyjádřit jako

\(\rho = \frac{n}{\cos{(\psi-\varphi)}}\),

kde \(n\) je vzdálenost přímky od počátku \(O\) a \(\psi\) je velikost orientovaného úhlu s vrcholem v počátku, jehož první rameno tvoří polární osa a druhé rameno polopřímka kolmá k přímce s počátkem v O.

Rovnice přímky určené bodem

Rovnice přímky se směrnicí \(k\) procházející bodem \([x_0,y_0]\) je

\(y-y_0=k(x-x_0)\)

Rovnice přímky procházející dvěma danými body \([x_1,y_1]\) a \([x_2,y_2]\), kde \(x_1\neq x_2\), má tvar

\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)

neboli

\(y-y_1 = (x-x_1) \frac{y_2-y_1}{x_2-x_1}\)

Předchozí rovnice bývá také vyjadřována ve formě determinantu

\(\begin{vmatrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \end{vmatrix} = 0\)

Tuto rovnici lze využít jako podmínku k určení, zda tři body \([x_1,y_1], [x_2,y_2], [x_3,y_3]\) leží na jedné přímce. Tyto body leží na jedné přímce, je-li splněna podmínka

\(\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} = 0\)

Prostorová přímka

Přímkou v prostoru se nazývá množina bodů prostoru, které vyhovují rovnici přímky. Rovnici přímky v prostoru lze vyjádřit různými způsoby.

Obecná rovnice přímky

V R³ lze přímku L definovat jako průsečík dvou rovin, pomocí soustavy jejich lineárních rovnic:

\(L=\{(x,y,z)\mid (a_1 x+b_1 y+c_1 z=d_1) \land (a_2 x+b_2 y+c_2 z=d_2)\}\)

(definici je nutné rozšířit o podmínky pro koeficienty \(a_1\) až \(d_2\), které zaručí, že roviny budou různoběžné). Přímka v prostoru je tedy řešením soustavy rovnic

\(a_1 x+b_1 y+c_1 z+d_1 = 0\)

\(a_2 x+b_2 y+c_2 z+d_2 = 0\)

Ve speciálním případě vyjádříme přímku jako průsečík dvou rovin, z nichž každá je kolmá k některé souřadnicové rovině, např. pro roviny kolmé k \(xy\) a \(xz\) dostaneme

\(y=mx+q\)

\(z=nx+r\)

Parametrické rovnice přímky

Parametrické rovnice přímky v prostoru mají tvar

\(x = x_0 + ta\)

\(y = y_0 + tb\)

\(z = z_0 + tc\)

kde \([x_0,y_0,z_0]\) je libovolný bod, kterým přímka prochází, \(a, b, c\) jsou konstanty určující směrnici přímky a \(t\in(-\infty,\infty)\) je parametr. Konstanty \(a, b, c\) mohou být vyjádřeny prostřednictvím směrových úhlů \(\alpha, \beta, \gamma\) jako

\(x = x_0 + t\cos\alpha\)

\(y = y_0 + t\cos\beta\)

\(z = z_0 + t\cos\gamma\)

Směrové úhly přitom splňují podmínku

\(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1\)

Rovnice přímky určené bodem

Rovnici přímky procházející body \([x_1,y_1,z_1], [x_2,y_2,z_2]\) lze zapsat jako

\(\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} = \frac{z-z_1}{z_2-z_1}\)

Rovnici přímky procházející bodem \([x_1,y_1,z_1]\) se směrovými úhly \(\alpha, \beta, \gamma\) lze zapsat jako

\(\frac{x-x_1}{\cos\alpha} = \frac{y-y_1}{\cos\beta} = \frac{z-z_1}{\cos\gamma}\)

Pokud místo směrových úhlů určíme směrnici přímky parametry \(a, b, c\), pak lze předchozí vztah přepsat jako

\(\frac{x-x_1}{a} = \frac{y-y_1}{b} = \frac{z-z_1}{c}\)

Přímka ve vícerozměrném prostoru

Přímku lze zavést také v n-rozměrném prostoru.

Parametrické vyjádření

Přímku v Rⁿ lze také vyjádřit parametricky: přímka procházející bodem \(A(a_1;a_2;...a_n) \,\) se směrovým vektorem \(v(v_1;v_2;...;v_n) \,\) je množina bodů \(L(x_1;x_2;...;x_n) \,\), pro které existuje skalár k takový, že

\(\left\{\begin{matrix} x_1 = a_1+kv_1 \\ x_2=a_2 + kv_2 \\ ... \\ x_n = a_n+kv_n \end{matrix}\right.\)

Vektorový tvar

Místo předchozího parametrického vyjádření lze použít vektorový zápis

\(\mathbf{x} = \mathbf{a} + k\mathbf{v}\)

Vzájemná poloha bodu a přímky

Tři nebo více bodů, které leží na téže přímce, se nazývají kolineární. Leží-li tři body na jedné přímce, pak vždy leží právě jeden z nich mezi ostatními dvěma. Leží-li bod \(B\) mezi body \(A\) a \(C\), pak bod \(B\) označíme jako vnitřní bod úsečky \(AC\). Bod \(X\) ležící na přímce \(p\) ji dělí na dvě polopřímky. Je-li bod \(A\) vnitřním bodem jedné z polopřímek, pak pro tuto polopřímku užíváme značení \(\begin{matrix} \rightarrow \\ XA \\ \end{matrix}\). Opačnou polopřímku k polopřímce \(\begin{matrix} \rightarrow \\ XA \\ \end{matrix}\) značíme \(\begin{matrix} \leftarrow \\ XA \\ \end{matrix}\).

Vzájemná poloha přímek

Dvě různé přímky ležící v téže rovině mohou být buď rovnoběžné a nikdy se neprotnout (nemají žádný společný bod), nebo různoběžné a protnout se v právě jednom bodě, průsečíku. Dvě roviny se protínají v nejvýše v jedné přímce, průsečnici. Ve vícerozměrných prostorech ale nemusí ani být rovnoběžné, ani se protínat, a říká se jim mimoběžky. Pokud jsou si obě přímky rovny, pak říkáme, že jde o přímky splývající (totožné). Přímku různoběžnou s rovnoběžkami \(p, q\) označujeme jako příčku rovnoběžek \(p, q\). Průnik dvou polopřímek \(\begin{matrix} \rightarrow \\ AB \\ \end{matrix}\) a \(\begin{matrix} \leftarrow \\ BA \\ \end{matrix}\) nazýváme úsečkou a značíme \(AB\).

Související články

• Základní geometrické útvary
• Lineární geometrické útvary
• Vzájemná poloha přímky a kružnice
• Výpočet průsečíku křivek

200 sociálních sítí a dalších služeb !
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii