V encyklopedii Allmultimedia.cz byl aktivován špičkový grafický skin Foreground.
Foreground plně podporuje – RWD, HTML 5.0, Super Galerii a YouTube 2.0 !
Foreground plně podporuje – RWD, HTML 5.0, Super Galerii a YouTube 2.0 !
Mocninná funkce
Z Multimediaexpo.cz
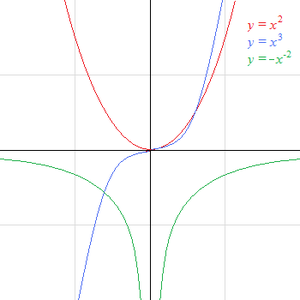
Mocninná funkce je elementární matematická funkce tvaru
- \(f\colon x \mapsto a x^r \qquad a,r \in \mathbb{R},\)
kde \(a\) a \(r\) jsou konstanty a \(x\) je proměnná.
Definiční obor
Definiční obor závisí na exponentu \(r\).
| \(r > 0\) | \(r < 0\) | |
|---|---|---|
| \(r \in \mathbb{Z}\) | \(\mathbb{R}\) | \(\mathbb{R}\setminus\{0\}\) |
| \(r \notin \mathbb{Z}\) | \(\mathbb{R}^+_0\) | \(\mathbb{R}^+\) |
Obor hodnot
Obor hodnot závisí na konstantě \(a\) a exponentu \(r\).
| \(r > 0\) | \(r < 0\) | |||
|---|---|---|---|---|
| \(r\) sudé nebo \(\notin \mathbb{Z}\) | \(r\) liché | \(r\) sudé nebo \(\notin \mathbb{Z}\) | \(r\) liché | |
| \(a > 0\) | \(\mathbb{R}^+_0\) | \(\mathbb{R}\) | \(\mathbb{R}^+\) | \(\mathbb{R}\setminus\{0\}\) |
| \(a < 0\) | \(\mathbb{R}^-_0\) | \(\mathbb{R}\) | \(\mathbb{R}^-\) | \(\mathbb{R}\setminus\{0\}\) |
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |