V pátek 26. dubna 2024 úderem 22 hodiny začíná naše nová
a opravdu velká série soutěží o nejlepší webovou stránku !!
Proto neváhejte a začněte hned zítra soutěžit o lákavé ceny !!

Průnik

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
m (Nahrazení textu „<math>“ textem „<big>\(“)
Řádka 4: Řádka 4:
== Formální definice ==
== Formální definice ==
-
Pro všechna ''x'' platí, že <math>x \in \left ( A  \cap B \right  ) \equiv \left ( x \in A \right  ) \and \left (x \in B \right ) </math>.
+
Pro všechna ''x'' platí, že <big>\(x \in \left ( A  \cap B \right  ) \equiv \left ( x \in A \right  ) \and \left (x \in B \right ) </math>.
-
V případě, že se jedná o průnik více množin, je možno jej chápat jako několik postupných průniků (viz ''asociativita'' níže), nebo tak, že prvek je součástí průniku právě tehdy, je-li prvkem všech množin. Obě tyto možnosti jsou však ekvivalentní. Např. pro průnik tří množin platí, že ''x'' ∈ ''A'' ∩ ''B'' ∩ ''C'' iff ''x'' ∈ ''A'' a zároveň ''x'' ∈ ''B'' a zároveň ''x'' ∈ ''C''. Průnik <math>n</math> množin <math>A_1, A_2, ..., A_n</math> lze zkráceně psát
+
V případě, že se jedná o průnik více množin, je možno jej chápat jako několik postupných průniků (viz ''asociativita'' níže), nebo tak, že prvek je součástí průniku právě tehdy, je-li prvkem všech množin. Obě tyto možnosti jsou však ekvivalentní. Např. pro průnik tří množin platí, že ''x'' ∈ ''A'' ∩ ''B'' ∩ ''C'' iff ''x'' ∈ ''A'' a zároveň ''x'' ∈ ''B'' a zároveň ''x'' ∈ ''C''. Průnik <big>\(n</math> množin <big>\(A_1, A_2, ..., A_n</math> lze zkráceně psát
-
<math>A_1 \cap A_2 \cap ... \cap A_2 = \bigcap_{i=_1}^n {A_i}</math>
+
<big>\(A_1 \cap A_2 \cap ... \cap A_2 = \bigcap_{i=_1}^n {A_i}</math>
Řádka 19: Řádka 19:
Průnik je [[Komutativita|komutativní]] operace, platí tedy, že ''A'' ∩ ''B'' = ''B'' ∩ ''A''.
Průnik je [[Komutativita|komutativní]] operace, platí tedy, že ''A'' ∩ ''B'' = ''B'' ∩ ''A''.
-
[[Neutrální prvek|Neutrálním prvkem]] pro operaci průniku je [[univerzum]], tzn. množina ''všech'' prvků, které v daném kontextu uvažujeme. Platí tedy <math>A \cap I = A</math>.
+
[[Neutrální prvek|Neutrálním prvkem]] pro operaci průniku je [[univerzum]], tzn. množina ''všech'' prvků, které v daném kontextu uvažujeme. Platí tedy <big>\(A \cap I = A</math>.
-
Výsledkem průniku množiny <math>A</math> s [[prázdná množina|prázdnou množinou]] je opět prázdná množina, tzn. <math>A \cap \emptyset = \emptyset</math>.
+
Výsledkem průniku množiny <big>\(A</math> s [[prázdná množina|prázdnou množinou]] je opět prázdná množina, tzn. <big>\(A \cap \emptyset = \emptyset</math>.
-
Je-li výsledkem průniku dvou množin <math>A,B</math> prázdná množina, pak platí <math>A \cap B \leftrightarrow B \subseteq -A</math>, kde <math>-A</math> je [[Doplněk množiny|dopňkem množiny]] <math>A</math>.
+
Je-li výsledkem průniku dvou množin <big>\(A,B</math> prázdná množina, pak platí <big>\(A \cap B \leftrightarrow B \subseteq -A</math>, kde <big>\(-A</math> je [[Doplněk množiny|dopňkem množiny]] <big>\(A</math>.
Vzhledem k definici průniku vyplývají všechny tyto skutečnosti z obdobných skutečností o [[Logická spojka|logické spojce]] ''a zároveň''.
Vzhledem k definici průniku vyplývají všechny tyto skutečnosti z obdobných skutečností o [[Logická spojka|logické spojce]] ''a zároveň''.
Řádka 29: Řádka 29:
[[Mohutnost]] průniku dvou množin je nejvýše rovna mohutnosti menší z nich: |''A'' ∩ ''B''| ≤ [[minimum|min]] { |''A''|, |''B''| }.
[[Mohutnost]] průniku dvou množin je nejvýše rovna mohutnosti menší z nich: |''A'' ∩ ''B''| ≤ [[minimum|min]] { |''A''|, |''B''| }.
-
Průnik je [[idempotence|idempotentní]], tzn. platí <math>A \cap A = A</math>.
+
Průnik je [[idempotence|idempotentní]], tzn. platí <big>\(A \cap A = A</math>.
== Související články ==
== Související články ==

Verze z 14. 8. 2022, 14:49

Průnik množin A a B

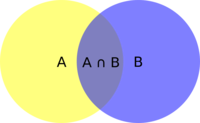
V matematice se jako průnik dvou nebo více množin označuje taková množina, která obsahuje pouze ty prvky, které se nalézají ve všech těchto množinách a obsahuje všechny takové prvky. Průnik množin A a B se označuje symbolem A ∩ B.

Formální definice

Pro všechna x platí, že \(x \in \left ( A \cap B \right ) \equiv \left ( x \in A \right ) \and \left (x \in B \right ) </math>.

V případě, že se jedná o průnik více množin, je možno jej chápat jako několik postupných průniků (viz asociativita níže), nebo tak, že prvek je součástí průniku právě tehdy, je-li prvkem všech množin. Obě tyto možnosti jsou však ekvivalentní. Např. pro průnik tří množin platí, že x ∈ A ∩ B ∩ C iff x ∈ A a zároveň x ∈ B a zároveň x ∈ C. Průnik \(n</math> množin \(A_1, A_2, ..., A_n</math> lze zkráceně psát

\(A_1 \cap A_2 \cap ... \cap A_2 = \bigcap_{i=_1}^n {A_i}</math>


Příklad: Průnikem množin { 1, 2, 5, 6, 8, 11 } a { 2, 3, 4, 6, 8, 9 } je množina { 2, 6, 8 }. Průnikem množin všech prvočísel { 2, 3, 5, 7, 11, … } a množiny sudých kladných čísel { 2, 4, 6, 8, … } je jednoprvková množina { 2 } (jelikož 2 je jediné sudé prvočíslo).

Vlastnosti

Operace průniku dvou množin (jakožto binární operace) je asociativní, tzn. (A ∩ B) ∩ C = A ∩ (B ∩ C). Současný průnik všech tří množin – A ∩ B ∩ C – je oběma těmto výrazům roven, proto je možno psát průnik libovolného množství množin bez použití závorek.

Průnik je komutativní operace, platí tedy, že A ∩ B = B ∩ A.

Neutrálním prvkem pro operaci průniku je univerzum, tzn. množina všech prvků, které v daném kontextu uvažujeme. Platí tedy \(A \cap I = A</math>.

Výsledkem průniku množiny \(A</math> s prázdnou množinou je opět prázdná množina, tzn. \(A \cap \emptyset = \emptyset</math>.

Je-li výsledkem průniku dvou množin \(A,B</math> prázdná množina, pak platí \(A \cap B \leftrightarrow B \subseteq -A</math>, kde \(-A</math> je dopňkem množiny \(A</math>.

Vzhledem k definici průniku vyplývají všechny tyto skutečnosti z obdobných skutečností o logické spojce a zároveň.

Mohutnost průniku dvou množin je nejvýše rovna mohutnosti menší z nich: |A ∩ B| ≤ min { |A|, |B| }.

Průnik je idempotentní, tzn. platí \(A \cap A = A</math>.

Související články


Citováno z „http://www.multimediaexpo.cz/mmecz/index.php/Pr%C5%AFnik“