V pátek 26. dubna 2024 úderem 22 hodiny začíná naše nová
a opravdu velká série soutěží o nejlepší webovou stránku !!
Proto neváhejte a začněte hned zítra soutěžit o lákavé ceny !!

Kolmice

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(++)
 
(Nejsou zobrazeny 2 mezilehlé verze.)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Kolmice|700}}
+
{{Upravit}}
-
 
+
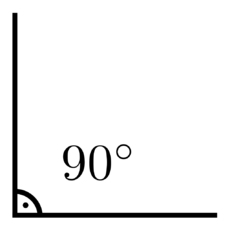
[[Soubor:Right angle dot.png|right|230px]]
 +
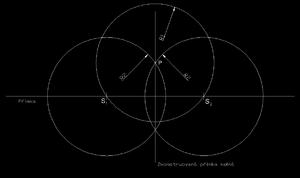
[[Soubor:Konstrukce kolmice.PNG|right|300px]]
 +
'''Kolmice''' je [[geometrie|geometrický]] útvar. Je to [[přímka]], která protíná jinou přímku a svírá s ní [[pravý úhel]], tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
 +
 
 +
O kolmicích lze mluvit i v případě [[polopřímka|polopřímek]] a [[úsečka|úseček]].
 +
 
 +
Kolmice je velmi důležitým geometrickým útvarem, neboť systémy čar složených z kolmic mají některé důležité vlastnosti z [[Ortogonalita|kolmosti]] (ortogonality) plynoucí.
 +
 
 +
Kolmici lze v rovině (třeba na papíře) nejsnadněji narýsovat pomocí [[Trojúhelník (rýsovací pomůcka)|trojúhelníku]] s ryskou a to tak, že se ryska přiloží na přímku a podle hrany trojúhelníku narýsujeme kolmici k této přímce.
 +
 
 +
Jde to ale také pomocí [[kružítko|kružítka]] a pravítka nebo trojúhelníku bez rysky. Na první přímce se zvolí dva různé body stejně daleko od bodu, kde se kolmice mají protínat. Tyto body pak poslouží jako středy pro kružnice s poloměry většími než je vzdálenost jejich středů od bodu průniku budoucích kolmic. Posléze již jen stačí spojit průniky takto vytvořených kružnic a kolmice na přímku je hotová.
 +
 
 +
Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou [[rovnoběžka|rovnoběžky]].
 +
 
 +
== Analytický výraz v komplexní rovině ==
 +
V [[ortonormalita|ortonormální]] [[soustava souřadnic|soustavě souřadnic]] je přímka ''a'' kolmicí na přímku ''b'', kde přímky ''a'' a ''b'' jsou vyjádřeny rovnicemi:
 +
* ''a'': y = ωx + a
 +
* ''b'': y = ω'x + b,
 +
pokud ω×ω'=-1.
 +
 
 +
Tyto rovnice i pojem [[vektorový prostor|vektorového prostoru]] dávají dobrý smysl jak pro [[Reálné číslo|reálná čísla]] tak pro [[komplexní čísla|komplexní]].
 +
 
 +
== Související články ==
 +
* [[Ortogonalita]]
 +
* [[Ortonormalita]]
 +
* [[Normála plochy]]
 +
 
 +
== Externí odkazy ==
 +
 
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]

Aktuální verze z 31. 8. 2023, 22:30

Broom icon.png Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte.
Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. 		Broom icon.png
Right angle dot.png
Konstrukce kolmice.PNG

Kolmice je geometrický útvar. Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.

O kolmicích lze mluvit i v případě polopřímek a úseček.

Kolmice je velmi důležitým geometrickým útvarem, neboť systémy čar složených z kolmic mají některé důležité vlastnosti z kolmosti (ortogonality) plynoucí.

Kolmici lze v rovině (třeba na papíře) nejsnadněji narýsovat pomocí trojúhelníku s ryskou a to tak, že se ryska přiloží na přímku a podle hrany trojúhelníku narýsujeme kolmici k této přímce.

Jde to ale také pomocí kružítka a pravítka nebo trojúhelníku bez rysky. Na první přímce se zvolí dva různé body stejně daleko od bodu, kde se kolmice mají protínat. Tyto body pak poslouží jako středy pro kružnice s poloměry většími než je vzdálenost jejich středů od bodu průniku budoucích kolmic. Posléze již jen stačí spojit průniky takto vytvořených kružnic a kolmice na přímku je hotová.

Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.

Analytický výraz v komplexní rovině

V ortonormální soustavě souřadnic je přímka a kolmicí na přímku b, kde přímky a a b jsou vyjádřeny rovnicemi:

  • a: y = ωx + a
  • b: y = ω'x + b,

pokud ω×ω'=-1.

Tyto rovnice i pojem vektorového prostoru dávají dobrý smysl jak pro reálná čísla tak pro komplexní.

Související články

Externí odkazy

Citováno z „http://www.multimediaexpo.cz/mmecz/index.php/Kolmice“