a opravdu velká série soutěží o nejlepší webovou stránku !!
Proto neváhejte a začněte hned zítra soutěžit o lákavé ceny !!
Hyperbola
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 3: | Řádka 3: | ||
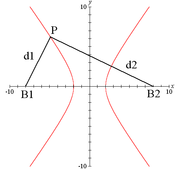
[[Image:Hyperbool.png|thumb|Ilustrace definice: ohniska (''B1'', ''B2''); bod hyperboly (''P''); vzdálenosti ohnisek (''d1'', ''d2'').]] | [[Image:Hyperbool.png|thumb|Ilustrace definice: ohniska (''B1'', ''B2''); bod hyperboly (''P''); vzdálenosti ohnisek (''d1'', ''d2'').]] | ||
'''Hyperbola''' je [[rovinná křivka]], [[kuželosečka]] s [[výstřednost]]í větší než 1. Lze ji také definovat jako [[množina|množinu]] všech [[bod]]ů v [[rovina|rovině]] o daném [[rozdíl]]u [[vzdálenost]]í od dvou pevných [[ohnisko|ohnisek]]. | '''Hyperbola''' je [[rovinná křivka]], [[kuželosečka]] s [[výstřednost]]í větší než 1. Lze ji také definovat jako [[množina|množinu]] všech [[bod]]ů v [[rovina|rovině]] o daném [[rozdíl]]u [[vzdálenost]]í od dvou pevných [[ohnisko|ohnisek]]. | ||
| - | Hyperbola také tvoří [[Graf (funkce)|graf funkce]] <big>\(y=1/x</ | + | Hyperbola také tvoří [[Graf (funkce)|graf funkce]] <big>\(y=1/x\)</big> v [[kartézská soustava souřadnic|kartézské soustavě souřadnic]]. |
Tvar hyperboly má dráha [[těleso|tělesa]] v poli [[centrální síla|centrální síly]] ([[gravitační pole|gravitační]] nebo [[elektrické pole]] vytvořené tělesem, které lze [[aproximace|aproximovat]] bodem - tuto aproximaci lze beze ztráty přesnosti udělat pro všechna [[sférická symetrie|sféricky symetrická]] tělesa pro [[prostor (geometrie)|prostor]] mimo jejich vnitřek), pokud je [[rychlost]] tohoto tělesa vyšší, než je [[úniková rychlost]]. | Tvar hyperboly má dráha [[těleso|tělesa]] v poli [[centrální síla|centrální síly]] ([[gravitační pole|gravitační]] nebo [[elektrické pole]] vytvořené tělesem, které lze [[aproximace|aproximovat]] bodem - tuto aproximaci lze beze ztráty přesnosti udělat pro všechna [[sférická symetrie|sféricky symetrická]] tělesa pro [[prostor (geometrie)|prostor]] mimo jejich vnitřek), pokud je [[rychlost]] tohoto tělesa vyšší, než je [[úniková rychlost]]. | ||
== Matematická vyjádření == | == Matematická vyjádření == | ||
'''Implicitní vyjádření''' | '''Implicitní vyjádření''' | ||
| - | : <big>\(\| F_1X \| - \| F_2X \| = 2a \,\!</ | + | : <big>\(\| F_1X \| - \| F_2X \| = 2a \,\!\)</big> |
| - | [[Množina]] všech [[bod]]ů X v [[rovina|rovině]], které mají od dvou různých [[ohnisko|ohnisek]] <big>\(F_1</ | + | [[Množina]] všech [[bod]]ů X v [[rovina|rovině]], které mají od dvou různých [[ohnisko|ohnisek]] <big>\(F_1\)</big> a <big>\(F_2\)</big> [[konstanta|konstantní]] (neměnnou) [[absolutní hodnota|absolutní hodnotu]] rozdílu [[vzdálenost]]í. |
=== Kartézský souřadnicový systém === | === Kartézský souřadnicový systém === | ||
Standardní popis hyperboly: <br /> | Standardní popis hyperboly: <br /> | ||
| Řádka 19: | Řádka 19: | ||
'''o<sub>2</sub>''' - vedlejší osa hyperboly <br /> | '''o<sub>2</sub>''' - vedlejší osa hyperboly <br /> | ||
'''p<sub>1</sub>, p<sub>2</sub>''' - [[asymptota|asymptoty]] hyperboly <br /> | '''p<sub>1</sub>, p<sub>2</sub>''' - [[asymptota|asymptoty]] hyperboly <br /> | ||
| - | <big>\(|AS| = |SB| = a \,\!</ | + | <big>\(|AS| = |SB| = a \,\!\)</big> - délka hlavní poloosy <br /> |
| - | <big>\(|CS| = |SD| = b \,\!</ | + | <big>\(|CS| = |SD| = b \,\!\)</big> - délka vedlejší poloosy <br /> |
| - | <big>\(|F_1S| = |F_2S| = \sqrt{a^2 + b^2} = e \,\!</ | + | <big>\(|F_1S| = |F_2S| = \sqrt{a^2 + b^2} = e \,\!\)</big> [[excentricita]] <br /> |
| - | <big>\(|AB| = 2a \,\!</ | + | <big>\(|AB| = 2a \,\!\)</big> - délka hlavní osy <br /> |
| - | <big>\(|CD| = 2b \,\!</ | + | <big>\(|CD| = 2b \,\!\)</big> - délka vedlejší osy <br /> |
'''X[x, y]''' - libovolný bod náležící hyperbole | '''X[x, y]''' - libovolný bod náležící hyperbole | ||
</div> | </div> | ||
| - | Pokud <big>\(a=b</ | + | Pokud <big>\(a=b\)</big>, pak dostáváme rovnici '''rovnoosé hyperboly'''. |
==== Charakteristické rovnice hyperboly dle jejího umístění ==== | ==== Charakteristické rovnice hyperboly dle jejího umístění ==== | ||
| - | *Hlavní osa <big>\(o_1</ | + | *Hlavní osa <big>\(o_1\)</big> hyperboly [[rovnoběžky|rovnoběžná]] s osou <big>\(x\)</big> |
:''Středová [[rovnice]]'': | :''Středová [[rovnice]]'': | ||
| - | :: <big>\({(x - m)^2\over a^2} - {(y - n)^2\over b^2} = 1 \,\!</ | + | :: <big>\({(x - m)^2\over a^2} - {(y - n)^2\over b^2} = 1 \,\!\)</big> |
:''Obecná rovnice'': | :''Obecná rovnice'': | ||
| - | :: <big>\(Ax^2 - By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!</ | + | :: <big>\(Ax^2 - By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!\)</big> |
:''Rovnice [[asymptota|asymptot]]'': | :''Rovnice [[asymptota|asymptot]]'': | ||
| - | :: <big>\(y - n = \pm{b\over a}(x - m) \,\!</ | + | :: <big>\(y - n = \pm{b\over a}(x - m) \,\!\)</big> |
| - | :''Rovnice [[tečna|tečny]] v bodě <big>\(T[x_0, y_0]</ | + | :''Rovnice [[tečna|tečny]] v bodě <big>\(T[x_0, y_0]\)</big>'': |
| - | :: <big>\({(x - m)(x_0 - m)\over a^2} - {(y - n)(y_0 - n)\over b^2} = 1 \,\!</ | + | :: <big>\({(x - m)(x_0 - m)\over a^2} - {(y - n)(y_0 - n)\over b^2} = 1 \,\!\)</big> |
| - | *Hlavní osa <big>\(o_1</ | + | *Hlavní osa <big>\(o_1\)</big> hyperboly rovnoběžná s osou <big>\(y\)</big> |
:''Středová rovnice'': | :''Středová rovnice'': | ||
| - | :: <big>\({(y - n)^2\over a^2} - {(x - m)^2\over b^2} = 1 \,\!</ | + | :: <big>\({(y - n)^2\over a^2} - {(x - m)^2\over b^2} = 1 \,\!\)</big> |
:''Obecná rovnice'': | :''Obecná rovnice'': | ||
| - | :: <big>\(- Ax^2 + By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!</ | + | :: <big>\(- Ax^2 + By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!\)</big> |
:''Rovnice [[asymptota|asymptot]]'': | :''Rovnice [[asymptota|asymptot]]'': | ||
| - | :: <big>\(y - n = \pm{a\over b}(x - m) \,\!</ | + | :: <big>\(y - n = \pm{a\over b}(x - m) \,\!\)</big> |
| - | :''Rovnice [[tečna|tečny]] v bodě <big>\(T[x_0, y_0]</ | + | :''Rovnice [[tečna|tečny]] v bodě <big>\(T[x_0, y_0]\)</big>: |
| - | :: <big>\({(y - n)(y_0 - n)\over a^2} - {(x - m)(x_0 - m)\over b^2} = 1 \,\!</ | + | :: <big>\({(y - n)(y_0 - n)\over a^2} - {(x - m)(x_0 - m)\over b^2} = 1 \,\!\)</big> |
| - | *[[asymptota|Asymptoty]] <big>\(p_1, p_2</ | + | *[[asymptota|Asymptoty]] <big>\(p_1, p_2\)</big> [[rovnoběžky|rovnoběžné]] s osami <big>\(x\)</big> a <big>\(y\)</big> |
[[Image:Función inversa.png|thumb|Asymptoty totožné s osami ''x'' a ''y'': ''y = 1/x'']] | [[Image:Función inversa.png|thumb|Asymptoty totožné s osami ''x'' a ''y'': ''y = 1/x'']] | ||
:''Středová rovnice'': | :''Středová rovnice'': | ||
| - | :: <big>\((x - m)(y - n) = c \,\!</ | + | :: <big>\((x - m)(y - n) = c \,\!\)</big><br /> |
| - | :: <big>\(a = b = \sqrt{2|c|} \,\!</ | + | :: <big>\(a = b = \sqrt{2|c|} \,\!\)</big> |
:''Obecná rovnice'': | :''Obecná rovnice'': | ||
| - | :: <big>\(xy + Ax + By + C = 0 \,\!</ | + | :: <big>\(xy + Ax + By + C = 0 \,\!\)</big> |
:''Rovnice asymptot'': | :''Rovnice asymptot'': | ||
| - | :: <big>\(x = m, y = n \,\!</ | + | :: <big>\(x = m, y = n \,\!\)</big> |
==== Převedení obecné rovnice na středovou ==== | ==== Převedení obecné rovnice na středovou ==== | ||
Uspořádáme členy v [[rovnice|rovnici]]. | Uspořádáme členy v [[rovnice|rovnici]]. | ||
| - | : <big>\(2x^2 + 4x - y^2 + 3y - {17\over 4} = 0 \,\!</ | + | : <big>\(2x^2 + 4x - y^2 + 3y - {17\over 4} = 0 \,\!\)</big> |
Z prvních dvou členů vytkneme dvojku ([[koeficient]]) a doplníme je na druhou [[mocnina|mocninu]] [[mnohočlen|dvojčlenu]]. To samé provedeme i u následujících dvou členů, s tím rozdílem, že vytkneme mínus. | Z prvních dvou členů vytkneme dvojku ([[koeficient]]) a doplníme je na druhou [[mocnina|mocninu]] [[mnohočlen|dvojčlenu]]. To samé provedeme i u následujících dvou členů, s tím rozdílem, že vytkneme mínus. | ||
| - | : <big>\(2\left[{(x + 1)}^2 - 1\right] -{\left[(y - {3\over 2}\right)}^2 - {9\over 4}] = {17\over 4} \,\!</ | + | : <big>\(2\left[{(x + 1)}^2 - 1\right] -{\left[(y - {3\over 2}\right)}^2 - {9\over 4}] = {17\over 4} \,\!\)</big> |
Dále upravujeme rovnici tak, aby odpovídala středovému tvaru. | Dále upravujeme rovnici tak, aby odpovídala středovému tvaru. | ||
| - | : <big>\(2(x + 1)^2 - 2 - {\left(y - {3\over 2}\right)}^2 + {9\over 4} = {17\over 4} \,\!</ | + | : <big>\(2(x + 1)^2 - 2 - {\left(y - {3\over 2}\right)}^2 + {9\over 4} = {17\over 4} \,\!\)</big> |
| - | : <big>\(2(x + 1)^2 - {\left(y - {3\over 2}\right)}^2 = 4 \,\!</ | + | : <big>\(2(x + 1)^2 - {\left(y - {3\over 2}\right)}^2 = 4 \,\!\)</big> |
| - | : <big>\({(x + 1)^2 \over 2} - {{\left(y - {3\over 2}\right)}^2 \over 4} = 1 \,\!</ | + | : <big>\({(x + 1)^2 \over 2} - {{\left(y - {3\over 2}\right)}^2 \over 4} = 1 \,\!\)</big> |
Z výsledné rovnice snadno zjistíme vlastnosti hyperboly.<br /> | Z výsledné rovnice snadno zjistíme vlastnosti hyperboly.<br /> | ||
| - | Jedná se o hyperbolu, jejíž hlavní osa <big>\(o_1</ | + | Jedná se o hyperbolu, jejíž hlavní osa <big>\(o_1\)</big> je rovnoběžná s osou <big>\(x\)</big>.<br /> |
| - | <big>\(S\left[-1, {3\over 2}\right] \,\!</ | + | <big>\(S\left[-1, {3\over 2}\right] \,\!\)</big>, <big>\(a = \sqrt{2} \,\!\)</big>, <big>\(b = 2 \,\!\)</big>, |
| - | <big>\(e = \sqrt{6} \,\!</ | + | <big>\(e = \sqrt{6} \,\!\)</big>, <big>\(p_1: y = \sqrt{2}x + {3 + 2\sqrt{2}\over 2 } \,\!\)</big>, <big>\(p_2: y = - \sqrt{2}x + {3 - 2\sqrt{2}\over 2 } \,\!\)</big> |
==== Vzájemná poloha hyperboly a přímky ==== | ==== Vzájemná poloha hyperboly a přímky ==== | ||
Řešíme [[soustava rovnic|soustavu rovnic]] hyperboly a [[přímka|přímky]]. | Řešíme [[soustava rovnic|soustavu rovnic]] hyperboly a [[přímka|přímky]]. | ||
| Řádka 73: | Řádka 73: | ||
s jednou z [[asymptota|asymptot]] - přímka je [[sečna|sečnou]] hyperboly s jedním [[průsečík]]em. | s jednou z [[asymptota|asymptot]] - přímka je [[sečna|sečnou]] hyperboly s jedním [[průsečík]]em. | ||
Pakliže [[lineární rovnice]] nemá žádné řešení - přímka není [[sečna]]. | Pakliže [[lineární rovnice]] nemá žádné řešení - přímka není [[sečna]]. | ||
| - | Pokud vyjde [[kvadratická rovnice]] a [[diskriminant]] <big>\(D</ | + | Pokud vyjde [[kvadratická rovnice]] a [[diskriminant]] <big>\(D\)</big> je: |
*D > 0 dvě řešení - přímka je sečna se dvěma průsečíky | *D > 0 dvě řešení - přímka je sečna se dvěma průsečíky | ||
*D = 0 jedno řešení - tečna s bodem dotyku | *D = 0 jedno řešení - tečna s bodem dotyku | ||
| Řádka 86: | Řádka 86: | ||
=== Polární souřadnicový systém === | === Polární souřadnicový systém === | ||
Pro hyperbolu se středem ''S'' umístěným v počátku platí rovnice: | Pro hyperbolu se středem ''S'' umístěným v počátku platí rovnice: | ||
| - | :<big>\(r^2 = {a^2b^2\over b^2 \cos^2 \theta - a^2 \sin^2 \theta } \,\!</ | + | :<big>\(r^2 = {a^2b^2\over b^2 \cos^2 \theta - a^2 \sin^2 \theta } \,\!\)</big> |
Pro hyperbolu s ohniskem ''F'' umístěným v počátku platí rovnice: | Pro hyperbolu s ohniskem ''F'' umístěným v počátku platí rovnice: | ||
| - | :<big>\(r = {a(e^2 -1)\over 1 - e \cos \theta } \,\!</ | + | :<big>\(r = {a(e^2 -1)\over 1 - e \cos \theta } \,\!\)</big> |
== Související články == | == Související články == | ||
*[[Geometrický útvar]] | *[[Geometrický útvar]] | ||
Aktuální verze z 14. 8. 2022, 14:52
Hyperbola je rovinná křivka, kuželosečka s výstředností větší než 1. Lze ji také definovat jako množinu všech bodů v rovině o daném rozdílu vzdáleností od dvou pevných ohnisek. Hyperbola také tvoří graf funkce \(y=1/x\) v kartézské soustavě souřadnic. Tvar hyperboly má dráha tělesa v poli centrální síly (gravitační nebo elektrické pole vytvořené tělesem, které lze aproximovat bodem - tuto aproximaci lze beze ztráty přesnosti udělat pro všechna sféricky symetrická tělesa pro prostor mimo jejich vnitřek), pokud je rychlost tohoto tělesa vyšší, než je úniková rychlost.
Obsah |
Matematická vyjádření
Implicitní vyjádření
- \(\| F_1X \| - \| F_2X \| = 2a \,\!\)
Množina všech bodů X v rovině, které mají od dvou různých ohnisek \(F_1\) a \(F_2\) konstantní (neměnnou) absolutní hodnotu rozdílu vzdáleností.
Kartézský souřadnicový systém
Standardní popis hyperboly:
S[m, n] - Střed hyperboly o souřadnicích m, n
F1, F2 - ohniska hyperboly
A, B - vrcholy hyperboly
o1 - hlavní osa hyperboly
o2 - vedlejší osa hyperboly
p1, p2 - asymptoty hyperboly
\(|AS| = |SB| = a \,\!\) - délka hlavní poloosy
\(|CS| = |SD| = b \,\!\) - délka vedlejší poloosy
\(|F_1S| = |F_2S| = \sqrt{a^2 + b^2} = e \,\!\) excentricita
\(|AB| = 2a \,\!\) - délka hlavní osy
\(|CD| = 2b \,\!\) - délka vedlejší osy
X[x, y] - libovolný bod náležící hyperbole
Pokud \(a=b\), pak dostáváme rovnici rovnoosé hyperboly.
Charakteristické rovnice hyperboly dle jejího umístění
- Hlavní osa \(o_1\) hyperboly rovnoběžná s osou \(x\)
- Středová rovnice:
- \({(x - m)^2\over a^2} - {(y - n)^2\over b^2} = 1 \,\!\)
- Obecná rovnice:
- \(Ax^2 - By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!\)
- Rovnice asymptot:
- \(y - n = \pm{b\over a}(x - m) \,\!\)
- Rovnice tečny v bodě \(T[x_0, y_0]\):
- \({(x - m)(x_0 - m)\over a^2} - {(y - n)(y_0 - n)\over b^2} = 1 \,\!\)
- Hlavní osa \(o_1\) hyperboly rovnoběžná s osou \(y\)
- Středová rovnice:
- \({(y - n)^2\over a^2} - {(x - m)^2\over b^2} = 1 \,\!\)
- Obecná rovnice:
- \(- Ax^2 + By^2 + Cx + Dy + E = 0\;, A > 0, B > 0 \,\!\)
- Rovnice asymptot:
- \(y - n = \pm{a\over b}(x - m) \,\!\)
- Rovnice tečny v bodě \(T[x_0, y_0]\):
- \({(y - n)(y_0 - n)\over a^2} - {(x - m)(x_0 - m)\over b^2} = 1 \,\!\)
- Asymptoty \(p_1, p_2\) rovnoběžné s osami \(x\) a \(y\)
- Středová rovnice:
- \((x - m)(y - n) = c \,\!\)
- \(a = b = \sqrt{2|c|} \,\!\)
- \((x - m)(y - n) = c \,\!\)
- Obecná rovnice:
- \(xy + Ax + By + C = 0 \,\!\)
- Rovnice asymptot:
- \(x = m, y = n \,\!\)
Převedení obecné rovnice na středovou
Uspořádáme členy v rovnici.
- \(2x^2 + 4x - y^2 + 3y - {17\over 4} = 0 \,\!\)
Z prvních dvou členů vytkneme dvojku (koeficient) a doplníme je na druhou mocninu dvojčlenu. To samé provedeme i u následujících dvou členů, s tím rozdílem, že vytkneme mínus.
- \(2\left[{(x + 1)}^2 - 1\right] -{\left[(y - {3\over 2}\right)}^2 - {9\over 4}] = {17\over 4} \,\!\)
Dále upravujeme rovnici tak, aby odpovídala středovému tvaru.
- \(2(x + 1)^2 - 2 - {\left(y - {3\over 2}\right)}^2 + {9\over 4} = {17\over 4} \,\!\)
- \(2(x + 1)^2 - {\left(y - {3\over 2}\right)}^2 = 4 \,\!\)
- \({(x + 1)^2 \over 2} - {{\left(y - {3\over 2}\right)}^2 \over 4} = 1 \,\!\)
Z výsledné rovnice snadno zjistíme vlastnosti hyperboly.
Jedná se o hyperbolu, jejíž hlavní osa \(o_1\) je rovnoběžná s osou \(x\).
\(S\left[-1, {3\over 2}\right] \,\!\), \(a = \sqrt{2} \,\!\), \(b = 2 \,\!\),
\(e = \sqrt{6} \,\!\), \(p_1: y = \sqrt{2}x + {3 + 2\sqrt{2}\over 2 } \,\!\), \(p_2: y = - \sqrt{2}x + {3 - 2\sqrt{2}\over 2 } \,\!\)
Vzájemná poloha hyperboly a přímky
Řešíme soustavu rovnic hyperboly a přímky. Jestliže vyjde lineární rovnice, která popisuje přímku rovnoběžnou s jednou z asymptot - přímka je sečnou hyperboly s jedním průsečíkem. Pakliže lineární rovnice nemá žádné řešení - přímka není sečna. Pokud vyjde kvadratická rovnice a diskriminant \(D\) je:
- D > 0 dvě řešení - přímka je sečna se dvěma průsečíky
- D = 0 jedno řešení - tečna s bodem dotyku
- D < 0 žádné řešení - přímka je nesečna
Vzájemná poloha hyperboly a bodu
Jestliže převedeme všechny členy rovnice hyperboly na levou stranu (anulujeme rovnici) a dosadíme souřadnice bodu, pak bude platit:
- výsledná hodnota = 0 bod náleží hyperbole
- výsledná hodnota > 0 bod se nachází ve vnější rovině hyperboly
- výsledná hodnota < 0 bod se nachází ve vnitřní rovině hyperboly
Polární souřadnicový systém
Pro hyperbolu se středem S umístěným v počátku platí rovnice:
- \(r^2 = {a^2b^2\over b^2 \cos^2 \theta - a^2 \sin^2 \theta } \,\!\)
Pro hyperbolu s ohniskem F umístěným v počátku platí rovnice:
- \(r = {a(e^2 -1)\over 1 - e \cos \theta } \,\!\)
Související články
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |