a opravdu velká série soutěží o nejlepší webovou stránku !!
Proto neváhejte a začněte hned zítra soutěžit o lákavé ceny !!
Kužel
Z Multimediaexpo.cz
m (1 revizi) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 7: | Řádka 7: | ||
== Kuželová plocha a prostor == | == Kuželová plocha a prostor == | ||
[[Soubor:kuzelovy_prostor.png|thumb|Kuželový prostor.]] | [[Soubor:kuzelovy_prostor.png|thumb|Kuželový prostor.]] | ||
| - | Mějme jednoduchou uzavřenou [[křivka|křivku]] < | + | Mějme jednoduchou uzavřenou [[křivka|křivku]] <big>\(k\)</big>, která leží v [[rovina|rovině]]. [[Bod]]y, které leží [[přímka|přímkách]] procházejících libovolným bodem křivky <big>\(k\)</big> a bodem <big>\(V\)</big> ležícím mimo rovinu křivky <big>\(k\)</big> tvoří '''kuželovou plochu'''. Část prostoru ohraničená kuželovou plochou se nazývá '''kuželový prostor'''. |
Kuželová plocha je [[množina]] bodů v [[prostor (geometrie)|prostoru]], která vznikne z kužele tím, že odstraním podstavu a každou [[úsečka|úsečku]] pláště (tj. spojnici vrcholu kužele s bodem hranice podstavy) prodloužím na [[přímka|přímku]]. Nejlepší představa je taková ,že se jedná o dva středově souměrné (podle vrcholu kužele) kornouty jdoucí do nekonečna. | Kuželová plocha je [[množina]] bodů v [[prostor (geometrie)|prostoru]], která vznikne z kužele tím, že odstraním podstavu a každou [[úsečka|úsečku]] pláště (tj. spojnici vrcholu kužele s bodem hranice podstavy) prodloužím na [[přímka|přímku]]. Nejlepší představa je taková ,že se jedná o dva středově souměrné (podle vrcholu kužele) kornouty jdoucí do nekonečna. | ||
=== Rovnice === | === Rovnice === | ||
| - | '''Kuželová plocha''' ('''[[kvadratická plocha|kvadratický]] kužel''') s vrcholem v počátku, která v [[rovina|rovině]] < | + | '''Kuželová plocha''' ('''[[kvadratická plocha|kvadratický]] kužel''') s vrcholem v počátku, která v [[rovina|rovině]] <big>\(z=c\)</big> prochází [[elipsa|elipsou]] <big>\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)</big> (tzv. ''[[řídící křivka]]''), má [[rovnice|rovnici]] |
| - | :< | + | :<big>\(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0\)</big> |
[[přímka|Přímky]], které tvoří povrch kužele se nazývají ''[[tvořící přímka|tvořící přímky]]''. | [[přímka|Přímky]], které tvoří povrch kužele se nazývají ''[[tvořící přímka|tvořící přímky]]''. | ||
Tato plocha je ''[[asymptotická plocha|asymptotickou plochou]]'' (''asymptotickým kuželem'') [[hyperboloid|hyperboloidů]] | Tato plocha je ''[[asymptotická plocha|asymptotickou plochou]]'' (''asymptotickým kuželem'') [[hyperboloid|hyperboloidů]] | ||
| - | :< | + | :<big>\(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=\pm 1\)</big> |
| - | Pro < | + | Pro <big>\(a=b\)</big> jde o rotační kužel s osou rotace <big>\(z\)</big>. |
| - | Kuželovou plochu s vrcholem v bodě < | + | Kuželovou plochu s vrcholem v bodě <big>\([x_0,y_0,z_0]\)</big> je vždy možné vyjádřit rovnicí |
| - | :< | + | :<big>\(F\left(\frac{x-x_0}{z-z_0},\frac{y-y_0}{z-z_0}\right)=0\)</big> |
== Vlastnosti == | == Vlastnosti == | ||
Pro [[objem]] kužele platí | Pro [[objem]] kužele platí | ||
| - | :< | + | :<big>\(V = \frac{1}{3} \cdot S_p \cdot v\)</big>, |
| - | kde < | + | kde <big>\(S_p\)</big> je [[obsah]] podstavy a <big>\(v\)</big> je výška kužele. |
== Rotační kužel == | == Rotační kužel == | ||
[[Soubor:Cone (geometry).png|thumb|Rotační kužel.]] | [[Soubor:Cone (geometry).png|thumb|Rotační kužel.]] | ||
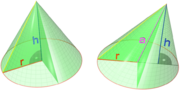
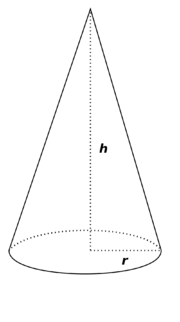
'''Rotační kužel''' je [[rotace (geometrie)|rotační]] [[těleso (geometrie)|těleso]] vzniklé otáčením [[pravoúhlý trojúhelník|pravoúhlého trojúhelníku]] v [[prostor (geometrie)|prostoru]] okolo jedné z [[odvěsna|odvěsen]]. Otáčením druhé odvěsny vznikne kruhová '''podstava kužele''' (někdy také nazývaná jako '''základna kužele'''), otáčením [[přepona|přepony]] pak '''kuželová plocha''' nebo jinak '''plášť kužele'''. Tento plášť je v podstatě „stočená“ [[kruhová výseč]], jejíž úhel záleží na poměru výšky kužele a [[poloměr]]u podstavy. Společný vrchol přepony a osy otáčení nazýváme '''vrchol kužele'''. | '''Rotační kužel''' je [[rotace (geometrie)|rotační]] [[těleso (geometrie)|těleso]] vzniklé otáčením [[pravoúhlý trojúhelník|pravoúhlého trojúhelníku]] v [[prostor (geometrie)|prostoru]] okolo jedné z [[odvěsna|odvěsen]]. Otáčením druhé odvěsny vznikne kruhová '''podstava kužele''' (někdy také nazývaná jako '''základna kužele'''), otáčením [[přepona|přepony]] pak '''kuželová plocha''' nebo jinak '''plášť kužele'''. Tento plášť je v podstatě „stočená“ [[kruhová výseč]], jejíž úhel záleží na poměru výšky kužele a [[poloměr]]u podstavy. Společný vrchol přepony a osy otáčení nazýváme '''vrchol kužele'''. | ||
=== Vlastnosti === | === Vlastnosti === | ||
| - | Označíme-li < | + | Označíme-li <big>\(r\)</big> [[poloměr]] kruhové podstavy kužele a <big>\(h\)</big> výšku kužele (t.j. vzdálenost vrcholu kužele od základny), pak lze vypočítat: |
* poloměr pláště (tj. vzdálenost vrcholu kužele od hraniční kružnice podstavy neboli délku strany pláště) pomocí [[Pythagorova věta|Pythagorovy věty]] jako | * poloměr pláště (tj. vzdálenost vrcholu kužele od hraniční kružnice podstavy neboli délku strany pláště) pomocí [[Pythagorova věta|Pythagorovy věty]] jako | ||
| - | :< | + | :<big>\( s = \sqrt{r^2 + h^2} \,\! \)</big> |
* [[objem]] kužele jako | * [[objem]] kužele jako | ||
| - | :< | + | :<big>\( V = \frac{\pi r^2 h}{3} \,\! \)</big> |
| - | * [[povrch]] kužele jako [[součet]] [[obsah]]u podstavy < | + | * [[povrch]] kužele jako [[součet]] [[obsah]]u podstavy <big>\( S_p = \pi r^2 \,\! \)</big> a obsahu pláště <big>\( S_{pl} = \pi r s \,\! \)</big> |
| - | :< | + | :<big>\( S = S_p + S_{pl} = \pi r (r + s) \,\! \)</big> |
* [[symetrie|Symetrické]] vlastnosti | * [[symetrie|Symetrické]] vlastnosti | ||
** Kužel není [[Středová souměrnost|středově souměrný]]. | ** Kužel není [[Středová souměrnost|středově souměrný]]. | ||
Aktuální verze z 14. 8. 2022, 14:52
Kužel je oblé těleso, které získáme jako průnik kuželového prostoru a rovinné vrstvy. Část kuželové plochy, která tvoří povrch kužele je označována jako plášť kužele. Řez kuželového prostoru hraniční rovinou vrstvy se nazývá podstava. Plášť kužele a podstavu nazýváme společným názvem povrch kužele. Bod, ve kterém se rovinný řez kužele redukuje na bod, se označuje jako vrchol kužele. Kolmou vzdálenost mezi podstavou a vrcholem nazýváme výškou kužele. Vzdálenost mezi vrcholem a podstavou podél pláště nazýváme stranou kužele. Je-li podstavou kužele kruh, pak jej označíme jako kruhový. Pokud kolmice spuštěná z vrcholu na rovinu podstavy prochází středem podstavy kruhového kužele, pak kužel označujeme jako rotační kužel nebo kolmý kruhový kužel. Pokud kruhový kužel není kolmý, pak jej označujeme jako kosý.
Obsah |
Kuželová plocha a prostor
Mějme jednoduchou uzavřenou křivku \(k\), která leží v rovině. Body, které leží přímkách procházejících libovolným bodem křivky \(k\) a bodem \(V\) ležícím mimo rovinu křivky \(k\) tvoří kuželovou plochu. Část prostoru ohraničená kuželovou plochou se nazývá kuželový prostor. Kuželová plocha je množina bodů v prostoru, která vznikne z kužele tím, že odstraním podstavu a každou úsečku pláště (tj. spojnici vrcholu kužele s bodem hranice podstavy) prodloužím na přímku. Nejlepší představa je taková ,že se jedná o dva středově souměrné (podle vrcholu kužele) kornouty jdoucí do nekonečna.
Rovnice
Kuželová plocha (kvadratický kužel) s vrcholem v počátku, která v rovině \(z=c\) prochází elipsou \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (tzv. řídící křivka), má rovnici
- \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0\)
Přímky, které tvoří povrch kužele se nazývají tvořící přímky. Tato plocha je asymptotickou plochou (asymptotickým kuželem) hyperboloidů
- \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=\pm 1\)
Pro \(a=b\) jde o rotační kužel s osou rotace \(z\). Kuželovou plochu s vrcholem v bodě \([x_0,y_0,z_0]\) je vždy možné vyjádřit rovnicí
- \(F\left(\frac{x-x_0}{z-z_0},\frac{y-y_0}{z-z_0}\right)=0\)
Vlastnosti
Pro objem kužele platí
- \(V = \frac{1}{3} \cdot S_p \cdot v\),
kde \(S_p\) je obsah podstavy a \(v\) je výška kužele.
Rotační kužel
Rotační kužel je rotační těleso vzniklé otáčením pravoúhlého trojúhelníku v prostoru okolo jedné z odvěsen. Otáčením druhé odvěsny vznikne kruhová podstava kužele (někdy také nazývaná jako základna kužele), otáčením přepony pak kuželová plocha nebo jinak plášť kužele. Tento plášť je v podstatě „stočená“ kruhová výseč, jejíž úhel záleží na poměru výšky kužele a poloměru podstavy. Společný vrchol přepony a osy otáčení nazýváme vrchol kužele.
Vlastnosti
Označíme-li \(r\) poloměr kruhové podstavy kužele a \(h\) výšku kužele (t.j. vzdálenost vrcholu kužele od základny), pak lze vypočítat:
- poloměr pláště (tj. vzdálenost vrcholu kužele od hraniční kružnice podstavy neboli délku strany pláště) pomocí Pythagorovy věty jako
- \( s = \sqrt{r^2 + h^2} \,\! \)
- objem kužele jako
- \( V = \frac{\pi r^2 h}{3} \,\! \)
- povrch kužele jako součet obsahu podstavy \( S_p = \pi r^2 \,\! \) a obsahu pláště \( S_{pl} = \pi r s \,\! \)
- \( S = S_p + S_{pl} = \pi r (r + s) \,\! \)
- Symetrické vlastnosti
- Kužel není středově souměrný.
- Kužel je osově souměrný podle spojnice vrcholu kužele se středem podstavy.
- Kužel je rovinově souměrný podle nekonečně mnoha rovin - rovinou souměrnosti je každá rovina, která v sobě obsahuje jeho osu (tj. vrchol a střed podstavy).
- V jistém smyslu je kužel „limitním případem“ posloupnosti pravidelných n-bokých jehlanů pro n jdoucí do nekonečna. To je ostatně vidět i ze vzorce pro objem, který je hodně podobný vzorci pro objem jehlanu.
Kuželosečky
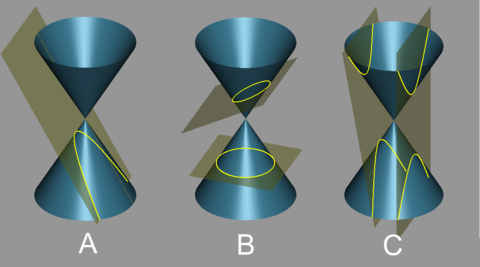
Z geometrického pohledu jsou zajímavé řezy rotační kuželové plochy, tj. průniky této plochy s nějakou rovinou. Singulární řezy kužele - pokud rovina řezu prochází vrcholem kužele, mohou nastat tři případy:
- průnikem je bod (vrchol kužele), pokud je úhel, který rovina řezu svírá s osou kužele, větší než úhel, který svírají přímky kuželové plochy s její osou
- průnikem je přímka ležící na kuželové ploše, pokud je úhel, který rovina řezu svírá s osou kužele rovný úhlu, který svírají přímky kuželové plochy s její osou
- průnikem jsou dvě přímky, které se protínají ve vrcholu kužele, pokud je úhel, který rovina řezu svírá s osou kužele, menší než úhel, který svírají přímky kuželové plochy s její osou (nebo v případě, kdy je rovina řezu rovnoběžná s osou kužele)
Regulární řezy kužele - pokud rovina řezu neprochází vrcholem kužele, mohou nastat čtyři případy:
- průnikem je kružnice, pokud je rovina řezu kolmá na osu kužele
- průnikem je elipsa, pokud je úhel, který rovina řezu svírá s osou kužele, větší než úhel, který svírají přímky kuželové plochy s její osou, ale rovina řezu není kolmá na osu kužele
- průnikem je parabola, pokud je úhel, který rovina řezu svírá s osou kužele rovný úhlu, který svírají přímky kuželové plochy s její osou
- průnikem je hyperbola, pokud je úhel, který rovina řezu svírá s osou kužele, menší než úhel, který svírají přímky kuželové plochy s její osou (nebo v případě, kdy je rovina řezu rovnoběžná s osou kužele)
To je důvod, proč jsou elipsa, parabola a hyperbola nazývány souhrnně kuželosečkami.
Související články
- Geometrický útvar
- Kvadratická plocha
- Oblá tělesa
- Mnohostěn
- Válec
- Jehlan
- Komolý kužel
- Elipsa
- Parabola
- Hyperbola
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |